How strong is 256-bit Encryption?
“It says 256-bit encryption strength… is that good?”
Most people see the term 256-bit encryption bandied about all the time and – if we’re being honest – have absolutely no idea what it means or how strong it is. Once you go beyond the surface-level, “it scrambles data and makes it unreadable,” encryption is an incredibly complicated subject. It’s not a light read. Most of us don’t keep a book about modular exponentiation on the end table beside our beds.
That’s why it’s understandable that there would be some confusion when it comes to encryption strengths, what they mean, what’s “good,” etc. There’s no shortage of questions about encryption – specifically 256-bit encryption.
Chief among them: How strong is 256-bit encryption?
So, today we’re going to talk about just that. We’ll cover what a bit of security even is, we’ll get into the most common form of 256-bit encryption and we’ll talk about just what it would take to crack encryption at that strength.
Let’s hash it out.
A quick refresher on encryption, in general
When you encrypt something, you’re taking the unencrypted data, called plaintext, and performing an algorithmic function on it to create a piece of encrypted ciphertext. The algorithm you’re using is called the key. With the exception of public keys in asymmetric encryption, the value of the encryption key needs to be kept a secret. The private key associated with that piece of ciphertext is the only practical means of decrypting it.
Now, that all sounds incredibly abstract, so let’s use an example. And we’ll leave Bob and Alice out of it, as they’re busy explaining encryption in literally every other example on the internet.
Let’s go with Jack and Diane, and let’s say that Jack wants to send Diane a message that says, “Oh yeah, life goes on.”
Jack’s going to take his message and he’s going to use an algorithm or cipher – the encryption key – to scramble the message into ciphertext. Now he’ll pass it along to Diane, along with the key, which can be used to decrypt the message so that it’s readable again.

As long as nobody else gets their hands on the key, the ciphertext is worthless because it can’t be read.
How does modern encryption work?
Jack and Diane just demonstrated encryption at its most basic form. And while the math used in primitive ciphers was fairly simple – owing to the fact it had to be performed by a human – the advent of computers has increased the complexity of the math that undergirds modern cryptosystems. But the concepts are still largely the same.
A key, or specific algorithm, is used to encrypt the data, and only another party with knowledge of the associated private key can decrypt it.
In this example, rather than a written message that bleakly opines that life continues even after the joy is lost, Jack and Diane are ‘doing the best they can’ on computers (still ‘holdin’ on to 16’ – sorry, these are John Mellencamp jokes that probably make no sense outside of the US). Now the encryption that’s about to take place is digital.

Jack’s computer will use its key, which is really an extremely complicated algorithm that has been derived from data shared by Jack and Diane’s devices, to encrypt the plaintext. Diane uses her matching symmetric key to decrypt and read the data.
But what’s actually getting encrypted? How do you encrypt “data?”
In the original example there were actual letters on a physical piece of paper that were turned into something else. But how does a computer encrypt data?
That goes back to the way that computers actually deal in data. Computers store information in binary form. 1’s and 0’s. Any data input into a computer is encoded so that it’s readable by the machine. It’s that encoded data, in its raw form, that gets encrypted. This is actually part of what goes into the different file types used by SSL/TLS certificates, it’s partially contingent on what type of encoding scheme you’re trying to encrypt.
Related: Secure Your Website with a Comodo SSL Certificate.
So Jack’s computer encrypts the encoded data and transmits it to Diane’s computer, which uses the associated private key to decrypt and read the data.

Again, as long as the private key stays, you know… private, the encryption remains secure.
Modern encryption has solved the biggest historical obstacle to encryption: key exchange. Historically, the private key had to be physically passed off. Key security was literally a matter of physically storing the key in a safe place. Key compromise not only rendered the encryption moot, it could get you killed.
In the 1970s a trio of cryptographers, Ralph Merkle, Whitfield Diffie and Martin Hellman, began working on a way to securely share an encryption key on an unsecure network with an attacker watching. They succeeded on a theoretical level, but were unable to come up with an asymmetric encryption function that was practical. They also had no mechanism for authenticating (but that’s a totally different conversation). Merkle came up with the initial concept, but his name is not associated with the key exchange protocol they invented – despite the protests of its other two creators.
About a year later Ron Rivest, Adi Shamir and Leonard Adleman created an eponymous key exchange method based on Diffie-Hellman key exchange (RSA), one that also included encryption/decryption and authentication functions. This is relevant because it was the birth of a whole new iteration of encryption: asymmetric encryption.
They also gave us the aforementioned Bob and Alice, which to me at least, makes it kind of a wash.
Anyway, understanding the difference between symmetric and asymmetric encryption is key to the rest of this discussion.
Asymmetric Encryption vs. Symmetric Encryption
Symmetric encryption is sometimes called private key encryption, because both parties must share a symmetric key that can be used to both encrypt and decrypt data.

Asymmetric encryption on the other hand is sometimes called public key encryption. A better way to think of asymmetric encryption might be to think of it like one-way encryption.
As opposed to both parties sharing a private key, there is a key pair. One party possess a public key that can encrypt, the other possesses a private key that can decrypt.

Asymmetric encryption is used primarily as a mechanism for exchanging symmetric private keys. There’s a reason for this, asymmetric encryption is historically a more expensive function owing to the size of its keys. So public key cryptography is used more as an external wall to help protect the parties as they facilitate a connection, while symmetric encryption is used within the actual connection itself.
2048-bit keys vs. 256-bit keys
In SSL/TLS, asymmetric encryption serves one, extremely important function. It lets the client encrypt the data that will be used by both parties to derive the symmetric session keys they’ll use to communicate. You could never use asymmetric encryption to functionally communicate. While the public key can be used to verify a digital signature, it can’t outright decrypt anything that the private key encrypts, hence we call asymmetric encryption “one way.”

But the bigger issue is the key size makes the actual encryption and decryption functions expensive in terms of the CPU resources they gobble up. This is why many larger organizations and enterprises, when deploying SSL/TLS at scale, offload the handshakes: to free up resources on their application servers.
Instead, we use symmetric encryption for the actual communication that occurs during an encrypted connection. Symmetric keys are smaller and less expensive to compute with.
So, when you see someone reference a 2048-bit private key, they’re most likely referring to an RSA private key. That’s an asymmetric key. It needs to be sufficiently resistant to attacks because it carries out such a critical function. Also, because key exchange is the best attack vector for compromising a connection. It’s much easier to steal the data used to create the symmetric session key and calculate it yourself than to have to crack the key by brute force after it’s already in use.
That begs the question: “How strong IS 256-bit encryption?” If it’s less robust than a 2048-bit key, is it still sufficient? And we’re going to answer that, but first we need to cover a little more ground for the sake of providing the right context.
What exactly is a “bit” of security?
It’s really important that we discuss bits of security and comparing encryption strength between algorithms before we actually get into any practical discussion of how strong 256 bits of security actually is. Because it’s not a 1:1 comparison.
For instance, a 128-bit AES key, which is half the current recommended size, is roughly equivalent to a 3072-bit RSA key in terms of the actual security they provide.
It’s also important to understand the difference between security claim and security level.
- Security Claim – This is the security level that cryptographic primitive – the cipher or hash function in question – was initially designed to achieve.
- Security Level – The ACTUAL strength that the cryptographic primitive achieves.
This is typically expressed in bits. A bit is a basic unit of information. It’s actually a portmanteau of “binary digit,” which is both incredibly efficient and also not so efficient. Sure, it’s easier to say bit. But I just spent an entire paragraph explaining that a bit is basically a 1 or a 0 in binary when the original term would’ve accomplished that in two words. So, you decide if it’s more efficient. Anyway, we’re not going to spend much more time on binary than we already have, but Ross wrote a great article on it a few months ago that you should check out.
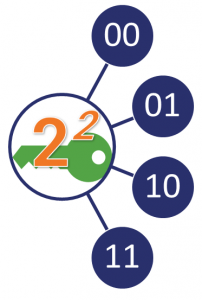
Anyway, security level and security claim are typically expressed in bits. In this context, the bits of security, let’s refer to that as (n) refers to the number operations an attacker would hypothetically need to perform to guess the value of the private key. The bigger the key, the harder it is to guess/crack. Remember, this key is in 1s and 0s, so there are two potential values for each bit. The attacker would have to perform 2n operations to crack the key.
That may be a bit too abstract so here’s a quick example: Let’s say there’s a 2-bit key. That means it will have 22 (4) values.
That would be trivially easy for a computer to crack, but when you start to get into larger key sizes it becomes prohibitively difficult for a modern computer to correctly guess the value of a private key in any reasonable amount of time.
But before we get to the math, let’s double back to security claim vs. security level
Security Claim vs. Security Level
Typically when you see encryption marketed, you’re seeing the Security Claim being advertised. That’s what the security level would be under optimal conditions. We’re going to keep this specific to SSL/TLS and PKI, but the percentage of time that the optimal conditions are present is far from 100%. Misconfigurations are commonplace, as is maintaining support for older versions of SSL/TLS and outmoded cipher suites for the sake of interoperability.
In the context of SSL/TLS, when a client arrives at a website a handshake takes place where the two parties determine a mutually agreed upon cipher suite to use. The encryption strength that you actually get is contingent upon the parameters decided on during the handshake, as well as the capabilities of the server and client themselves.
Taking a Closer Look at the SSL/TLS Handshake
There’s a lot going on underneath the hood when you connect to a website via HTTPS. First and foremost, everyone needs to… shake hands?!
Sometimes 256-bit encryption only provides a security level of 128 bits. This is particularly common with hashing algorithms, which measure resistance to two different types of attacks:
- Collisions – Where two different pieces of data produce the same hash value it’s called a collision and it breaks the algorithm.
- PreImage resistance – How resistant and algorithm is to an exploit where an attacker tries to find a message with a specific hash value.
So, for instance, SHA-256 has collision resistance of 128 bits (n/2) , but PreImage resistance of 256 bits. Obviously, hashing is different from encryption but there are also plenty of similarities that make it worth mentioning.
So, how strong is 256-bit encryption?
Again, this varies based on the algorithm you’re using, and it varies from asymmetric to symmetric encryption. As we said, these aren’t 1:1 comparisons. In fact, asymmetric encryption security level isn’t really as scientific as it might seem like it should be. Asymmetric encryption is based on mathematical problems that are easy to perform one way (encryption) but exceedingly difficult to reverse (decryption). Due to that, attacks against public key, asymmetric cryptosystems are typically much faster than the brute-force style searches for key space that plague private key, symmetric encryption schemes. So, when you’re talking about the security level of public key cryptography, it’s not a set figure, but a calculation of the implementation’s computational hardness against the best, most currently well-known attack.

Symmetric encryption strength is a little easier to calculate owing to the nature of the attacks they have to defend against.
So, let’s look at AES or Advanced Encryption Standard, which is commonly used as a bulk cipher with SSL/TLS. Bulk ciphers are the symmetric cryptosystems that actually handle securing the communication that occurs during an encrypted HTTPS connection.
There are historically two flavors: block ciphers and stream ciphers.
Block ciphers break everything they encrypt down into key-sized blocks and encrypts them. Decrypting involves piecing the blocks back together. And if the message is too short or too long, which is the majority of the time, they have to be broken up and/or padded with throwaway data to make them the appropriate length. Padding attacks are one of the most common threats to SSL/TLS.
TLS 1.3 did away with this style of bulk encryption for exactly that reason, now all ciphers must be set to stream mode. Stream ciphers encrypt data in pseudorandom streams of any length, they’re considered easier to deploy and require fewer resources. TLS 1.3 has also done away with some insecure stream ciphers, like RC4, too.
So, long story short, there are really only two suggested bulk ciphers nowadays, AES and ChaCha20. We’re going to focus on AES right now because ChaCha20 is a different animal.
TLS 1.2 Recommended Ciphers
- TLS_ECDHE_ECDSA_WITH_AES_256_GCM_SHA384
- TLS_ECDHE_ECDSA_WITH_AES_128_GCM_SHA256
- TLS_ECDHE_ECDSA_WITH_CHACHA20_POLY1305
- TLS_ECDHE_RSA_WITH_AES_256_GCM_SHA384
- TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256
- TLS_ECDHE_RSA_WITH_CHACHA20_POLY1305
TLS 1.3 Recommended Ciphers
- TLS_AES_256_GCM_SHA384
- TLS_CHACHA20_POLY1305_SHA256
- TLS_AES_128_GCM_SHA256
- TLS_AES_128_CCM_8_SHA256
- TLS_AES_128_CCM_SHA256
GCM stands for Galois Counter Mode, which allows AES – which is actually a block cipher – run in stream mode. CCM is similar, combing a counter mode with a message authentication functions.
As we covered, you can actually safely run AES in GCM or CCM with 128-bit keys and be fine. You’re getting equivalent of 3072-bit RSA in terms of the security level. But we typically suggest going with 256-bit keys so that you maintain maximum computational hardness for the longest period of time.

So, let’s look at those 256-bit keys. A 256-bit key can have 2256 possible combinations. As we mentioned earlier, a two-bit key would have four possible combinations (and be easily crackable by a two-bit crook). We’re dealing in exponentiation here though, so each time you raise the exponent, n, you increase the number of possible combinations wildly. 2256 is 2 x 2, x 2, x 2… 256 times.
As we’ve covered, the best way to crack an encryption key is ‘brute-forcing,’ which is basically just trial & error in simple terms. So, if the key length is 256-bit, there would be 2256 possible combinations, and a hacker must try most of the 2256 possible combinations before arriving at the conclusion. It likely won’t take all trying all of them to guess the key – typically it’s about 50% – but the time it would take to do this would last way beyond any human lifespan.
A 256-bit private key will have 115,792,089,237,316,195,423,570,985,008,687,907,853,269,
984,665,640,564,039,457,584,007,913,129,639,936 (that’s 78 digits) possible combinations. No Super Computer on the face of this earth can crack that in any reasonable timeframe.
Even if you use Tianhe-2 (MilkyWay-2), the fastest supercomputer in the world, it will take millions of years to crack 256-bit AES encryption.
That figure sky-rockets even more when you try to figure out the time it would take to factor an RSA private key. A 2048-bit RSA key would take 6.4 quadrillion years (6,400,000,000,000,000 years) to calculate, per DigiCert.
Nobody has that kind of time.
Quantum Computing is going to change all of this
Now would actually be a good spot to talk a little bit about quantum encryption and the threat it poses to our modern cryptographic primitives. As we’ve just covered, computers work in binary. 1’s and 0’s. And the way bits work on modern computers is that they have to be a known value, they’re either a 1 or a 0. Period. That means that a modern computer can only guess once at a time.

Obviously, that severely limits how quickly it can brute force combinations in an effort to crack a private key.
Quantum Computers will have no such limitations. Now, two things, first of all quantum computing is still about 7-10 years from viability, so we’re still a ways off. Some CAs, like DigiCert, have begun to put post-quantum digital certificates on IoT devices that will have long lifespans to try and preemptively secure them against quantum computing, but other than that we’re still in the research phase when it comes to quantum-proof encryption.
The issue is that quantum computers don’t use bits, they use quantum bits or qubits. A quantum bit can be BOTH a 1 and a 0 thanks to a principle called superposition, which is a little more complicated than we’re going to get today. Qubits give quantum computers the power to exponentiate their brute force attacks, which effectively cancels out the computational hardness provided by the exponentiation that took place with the cryptographic primitive. A four Qubit computer can effectively be in four different positions (22) at once. It’s 2n once again, so a Quantum Computer with n qubits can try 2n combinations simultaneously. Bristlecone, which has 72 qubits, can try 272 (4,722,366,482,869,645,213,696) values at once.
Again, we’re still a ways from that and the quantum computer would have to figure out how to successfully run Shor’s algorithm, another topic for another day, so this is still largely theoretical.
Still, suddenly 4.6 quadrillion years doesn’t seem like such a long time.
Let’s wrap this up…
256-bit encryption is fairly standard in 2019, but every mention of 256-bit encryption doesn’t refer to the same thing. Sometimes 256-bits of encryption only rises to a security level of 128 bits. Sometimes key size and security level are intrinsically linked while other times one is just used to approximate the other.
So the answer to “how strong is 256 bit encryption” isn’t one with a clear cut answer. At least not all time the time.
In the context of SSL/TLS though, it most commonly refers to AES encryption, where 256 bits really does mean 256 bits. And, at least for the time being, that 256-bit encryption is still plenty strong.
By the time an attacker using a modern computer is able to crack a 256-bit symmetric key, not only will it have been discarded, you’ll have likely replaced the SSL/TLS certificate that helped generate it, too.
Long story short, the biggest threat to your encryption and your encryption keys is still mismanagement, the technology behind them is sound.
As always, leave any comments or questions below…

This article was originally written by Jay Thakkar in 2017, it has been re-written for 2019 by Patrick Nohe.




































![A Look at 30 Key Cyber Crime Statistics [2023 Data Update]](https://www.thesslstore.com/blog/wp-content/uploads/2022/02/cyber-crime-statistics-feature2-75x94.jpg)





 (5 votes, average: 4.00 out of 5, rated)
(5 votes, average: 4.00 out of 5, rated)






5 Ways to Determine if a Website is Fake, Fraudulent, or a Scam – 2018
in Hashing Out Cyber SecurityHow to Fix ‘ERR_SSL_PROTOCOL_ERROR’ on Google Chrome
in Everything EncryptionRe-Hashed: How to Fix SSL Connection Errors on Android Phones
in Everything EncryptionCloud Security: 5 Serious Emerging Cloud Computing Threats to Avoid
in ssl certificatesThis is what happens when your SSL certificate expires
in Everything EncryptionRe-Hashed: Troubleshoot Firefox’s “Performing TLS Handshake” Message
in Hashing Out Cyber SecurityReport it Right: AMCA got hacked – Not Quest and LabCorp
in Hashing Out Cyber SecurityRe-Hashed: How to clear HSTS settings in Chrome and Firefox
in Everything EncryptionRe-Hashed: The Difference Between SHA-1, SHA-2 and SHA-256 Hash Algorithms
in Everything EncryptionThe Difference Between Root Certificates and Intermediate Certificates
in Everything EncryptionThe difference between Encryption, Hashing and Salting
in Everything EncryptionRe-Hashed: How To Disable Firefox Insecure Password Warnings
in Hashing Out Cyber SecurityCipher Suites: Ciphers, Algorithms and Negotiating Security Settings
in Everything EncryptionThe Ultimate Hacker Movies List for December 2020
in Hashing Out Cyber Security Monthly DigestAnatomy of a Scam: Work from home for Amazon
in Hashing Out Cyber SecurityThe Top 9 Cyber Security Threats That Will Ruin Your Day
in Hashing Out Cyber SecurityHow strong is 256-bit Encryption?
in Everything EncryptionRe-Hashed: How to Trust Manually Installed Root Certificates in iOS 10.3
in Everything EncryptionHow to View SSL Certificate Details in Chrome 56
in Industry LowdownPayPal Phishing Certificates Far More Prevalent Than Previously Thought
in Industry Lowdown